CSES Introductory Problem Solutions
It’s recommended to read and follow the book before looking for solutions and trying your best first. This article should be your last resort.
Anyone starting the competitive programming journey would have easily stumbled across the CSES Problem Set.
I will try to summarize the solutions as briefly as I can, leaving some for your imagination.
The implementation would be in c++, I will show only the actual implementation inside the main function and leave out the boilerplate code.
1. Weird Algorithm
Time Complexity: \(O(log(N))\)
Just do what is told, using a while loop would be the easiest but it can be implemented using for or do while
1
2
3
4
5
6
7
8
9
10
11
12
13
14
long long n;
cin >> n;
while (n != 1) {
cout << n << " ";
if (n % 2) {
n = n * 3 + 1;
} else {
n /= 2;
}
}
cout << 1 << "\n";
2. Missing Number
Time Complexity: \(O(N)\)
There are multiple ways to do it, two of them are listed below:
- Subtract the sum of inputs from \(O(N * (N + 1) / 2)\) (sum of first \(N\) natural numbers)
1
2
3
4
5
6
7
8
9
long long n;
cin >> n;
long long sum = n * (n + 1) / 2;
for (int i = 0; i < n - 1; i++) {
int temp;
cin >> temp;
sum -= temp;
}
cout << sum << "\n";
- Use the XOR property. \(a\)^\(a = 0\). So XOR for all the inputs with XOR of all the number from \(1\) to \(N\), the ending result will contain only the missing number;
1
2
3
4
5
6
7
8
9
10
11
long long n;
cin >> n;
long long allXor = n, inputXor = 0;
for (int i = 1; i <= n - 1; i++) {
int temp;
cin >> temp;
inputXor ^= temp;
allXor ^= i;
}
cout << (allXor ^ inputXor) << "\n";
3. Repetitions
Time Complexity: \(O(N)\)
Loop through the string, if the current character is same as the last character increase the size of current segment, if it is different then start a new segment. Maximum of all the segements would be the answer. Have extra variables to store all the different values
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
string s;
cin >> s;
int cnt = 1, ans = 1;
char prev = '$';
for (char x: s) {
if (x == prev) {
cnt++;
ans = max(ans, cnt);
} else {
ans = max(ans, cnt);
cnt = 1;
}
prev = x;
}
cout << ans << "\n";
4. Increasing Array
Time Complexity: \(O(N)\)
First observation is you don’t need to increase the first element in the array. You need to increase the elements atleast equal to the previous elements. So loop from left to right and keep making the current element as big as the previous elements.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int n;
cin >> n;
long long prev = 0, curr;
long long ans = 0;
for (int i = 0; i < n; i++) {
cin >> curr;
if (curr < prev) {
ans += prev - curr;
curr = prev;
}
prev = curr;
}
cout << ans << "\n";
5. Permutations
Time Complexity: \(O(N)\)
It can have multiple solutions, the solution I came up with was output even numbers and then output odd numbers. There are some special cases so beware!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int n;
cin >> n;
if (n == 1) {
cout << 1 << "\n";
}
else if (n < 4) {
cout << "NO SOLUTION\n";
}
else if (n == 4) {
cout << "3 1 4 2\n";
}
else {
int ptr = 1;
while (ptr <= n) {
cout << ptr << " ";
ptr += 2;
}
ptr = 2;
while (ptr <= n) {
cout << ptr << " ";
ptr += 2;
}
}
6. Number Spiral
Time Complexity: \(O(1)\)
This problem requires observation. Divide your cases, \(x > y\), \(x == y\) and \(x < y\). You need to some case work what the answer is and focus on how the spiral affects the answer
1
// Try yourself
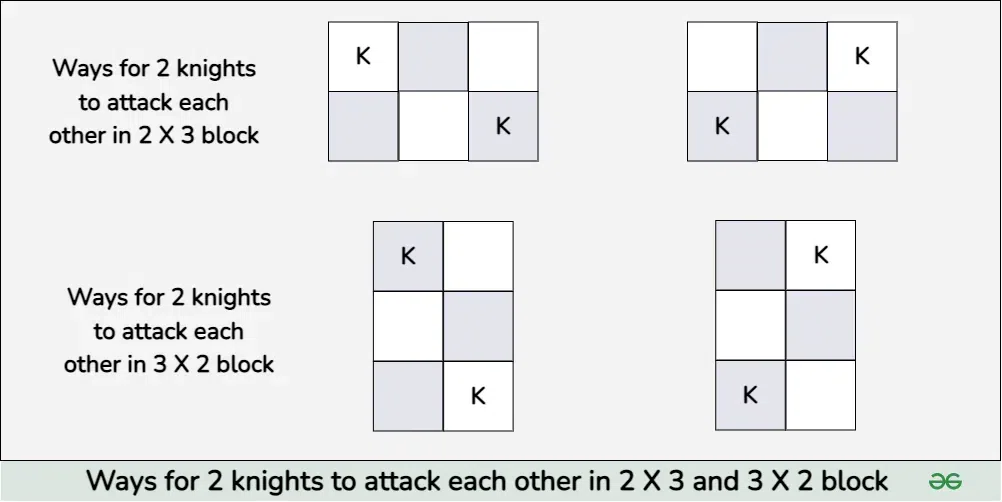
7. Two Knights
Time Complexity: \(O(N)\)
In this problem, instead of find the total number of possible combinations it would be better to count total number of invlid combinations and substract it from all the possible combinations.
- All the possible combinations are \(O(N * (N - 1) / 2)\) where \(N\) is the total number of squares which would be \(K^2\).
- Number of ways they attack each other would be, number of ways to place a \(2 * 3\) sized rectangle. Work out this math yourself !
1
2
3
4
5
6
7
8
long long n;
cin >> n;
for (long long k = 1; k <= n; k++) {
long long N = k * k;
long long tot = N * (N - 1) / 2;
long long invalid = (k - 1) * (k - 2) * 4;
cout << max(0LL, tot - invalid) << "\n";
}
8. Two Sets
Time Complexity: \(O(N)\)
Let remove the impossible case. When the sum of elements is odd then we cannot divide it into two sets. So now we have cases where the sum is even.
Lets take small cases \(N\) equal to \(1\) and \(2\) are not possible.
\(N = 3\): The sets can be \(\{1, 2\}\) and \(\{3\}\)
\(N = 4\): The sets can be \(\{1, 4\}\) and \(\{2, 3\}\)
We know that 4 consecutive numbers can be divided into two sets of equal sum. That is the idea ! There are only two cases for \(N % 4\) which are \(0, 3\). Try figuring out why remainder 1 and 2 are not possible (hint is that we elimated odd over all sum).
Rest is just implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
long long n;
cin >> n;
long long sum = n * (n + 1) / 2;
if (sum % 2)
{
cout << "NO\n";
return;
}
sum /= 2;
vector<int> st1, st2;
if (n % 4 == 0)
{
for (int i = 1; i < n; i += 4)
{
st1.push_back(i);
st1.push_back(i + 3);
st2.push_back(i + 1);
st2.push_back(i + 2);
}
}
else if (n % 4 == 3)
{
st1.push_back(1);
st1.push_back(2);
st2.push_back(3);
for (int i = 4; i < n; i += 4)
{
st1.push_back(i);
st1.push_back(i + 3);
st2.push_back(i + 1);
st2.push_back(i + 2);
}
}
cout << "YES\n";
cout << st1.size() << "\n";
for (int x : st1)
{
cout << x << " ";
}
cout << "\n";
cout << st2.size() << "\n";
for (int x : st2)
{
cout << x << " ";
}
cout << "\n";
9. Bit Strings
Time Complexity: \(O(log(N))\)
The answer is \(2^n\) !
1
2
3
4
5
6
7
8
9
10
11
long long mod = 1e9 + 7;
long long res = 1;
long long n;
cin >> n;
while (n--) {
res *= 2;
res %= mod;
}
cout << res << "\n";
10. Trailing Zeros
Time Complexity: \(O(log(N))\)
A zero comes from \(10\), \(10\). Ten comes from \(2\) and \(5\). So calculate the number of elements that contain \(2\) and \(5\) as factor and minimum of them would be the number of zeros.
We need to also consider all the powers of \(2\) as well as \(5\), number which have more that one factor of them.
Also it can be seen \(5\) will always be in lesser number, so just calculate the total power of \(5\) in the factorial.
1
2
3
4
5
6
7
8
9
10
11
12
long long n;
cin >> n;
long long ans = 1;
long long pwr = 5;
long long ans = 0;
while (pwr <= n) {
ans += (n / pwr);
pwr *= 5;
}
cout << ans << "\n";
11. Coin Piles
Time Complexity: \(O(1)\)
Lets say you make the first move \(x\) times and the second move \(y\) times. So, to satisfy the conditions you have the following two equations
- \[a - x - 2 * y = 0\]
- \[b - y - 2 * x = 0\]
Re arrange the values and you get
- \[x = (2 * b - a) / 3\]
- \[y = (2 * a - b) / 3\]
Now just verify that the values of \(x\) and \(y\) are both positive and integers
1
2
3
4
5
6
7
8
9
10
11
12
13
14
ll a, b;
cin >> a >> b;
ll x = 2 * b - a;
ll y = 2 * a - b;
if ((x < 0) || (x % 3) || (y < 0) || (y % 3))
{
cout << "NO\n";
}
else
{
cout << "YES\n";
}
12. Palindrome Reorder
Time Complexity: \(O(N)\)
Keep pairing same characters. If there are more that two character that are singled out then there is no solution, else there is a solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
vector<int> freq(26, 0);
string s;
cin >> s;
for (char x : s)
{
freq[x - 'A']++;
}
int odd = -1;
string ans;
for (int i = 0; i < 26; i++)
{
if (freq[i] % 2)
{
if (odd == -1)
{
odd = i;
}
else
{
cout << "NO SOLUTION\n";
return;
}
}
ans += string(freq[i] / 2, (char)('A' + i));
}
cout << ans;
if (odd != -1)
{
cout << (char)('A' + odd);
}
reverse(ans.begin(), ans.end());
cout << ans << "\n";
13. Gray Code
Time Complexity:
TBD
14. Tower of Hanoi
Time Complexity:
TBD
15. Creating Strings
Time Complexity: \(O(N!)\)
Just brute force the solution my taking all the permutation. Since the length of string is \(8\), \(8!\) is well below time limit. For permutation using the inbuild stl library method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
string s;
cin >> s;
vector<string> store;
sort(s.begin(), s.end());
do
{
store.push_back(s);
} while (next_permutation(s.begin(), s.end()));
cout << store.size() << "\n";
for (string x : store)
{
cout << x << "\n";
}
16. Apple Division
Time Complexity: \(O(2^N)\)
Observe that \(N\) is small \(<= 20\). So just generate all the subsets and brute force the solution:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
long long n;
cin >> n;
vector<long long> arr(n);
long long ans = 0;
for (int i = 0; i < n; i++)
{
cin >> arr[i];
ans += arr[i];
}
for (int i = 0; i < (1 << 20); i++)
{
long long diff = 0;
for (int j = 0; j < n; j++)
{
if (i & (1 << j))
{
diff += arr[j];
}
else
{
diff -= arr[j];
}
}
ans = min(ans, abs(diff));
}
cout << ans << "\n";
17. Chessboard and Queens
Time Complexity: \(O(8!)\)
Just brute force the solution. Start placing the Queens one by one and check if the configuration is correct. Once all the queens are placed increament the answer. The implementation for the solution is the hard part.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
int cntr = 0;
vector<string> arr(8);
map<int, int> row, col, dia, odia;
void solve(int n)
{
if (n == 8)
{
cntr++;
return;
}
for (int j = 0; j < 8; j++)
{
if (arr[n][j] != '*' && !row[n] && !col[j] && !dia[n + j] && !odia[n - j])
{
row[n] = col[j] = dia[n + j] = odia[n - j] = 1;
solve(n + 1);
row[n] = col[j] = dia[n + j] = odia[n - j] = 0;
}
}
}
int main()
{
for (int i = 0; i < 8; i++)
{
cin >> arr[i];
}
solve(0);
cout << cntr << "\n";
}
18. Digit Queries
Time Complexity:
TBD
19. Grid Paths
This problem is very well discussed in the CSES book, use the optimizations:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
int ans = 0;
string s;
int vis[10][10];
bool check(int i, int j)
{
if (i >= 1 && i <= 7 && j >= 1 && j <= 7)
{
if (vis[i][j])
return false;
if (vis[i - 1][j] && vis[i + 1][j] && !vis[i][j - 1] && !vis[i][j + 1])
return false;
if (!vis[i - 1][j] && !vis[i + 1][j] && vis[i][j - 1] && vis[i][j + 1])
return false;
return true;
}
return false;
}
void solve(int i, int j, int pos)
{
if (i == 7 && j == 1)
{
ans += (pos == s.size());
return;
}
vis[i][j] = 1;
if (s[pos] == '?')
{
// choose any
if (check(i, j - 1))
{
solve(i, j - 1, pos + 1);
}
if (check(i, j + 1))
{
solve(i, j + 1, pos + 1);
}
if (check(i - 1, j))
{
solve(i - 1, j, pos + 1);
}
if (check(i + 1, j))
{
solve(i + 1, j, pos + 1);
}
}
else
{
if (s[pos] == 'L')
{
if (check(i, j - 1))
{
solve(i, j - 1, pos + 1);
}
}
else if (s[pos] == 'R')
{
if (check(i, j + 1))
{
solve(i, j + 1, pos + 1);
}
}
else if (s[pos] == 'U')
{
if (check(i - 1, j))
{
solve(i - 1, j, pos + 1);
}
}
else if (s[pos] == 'D')
{
if (check(i + 1, j))
{
solve(i + 1, j, pos + 1);
}
}
}
vis[i][j] = 0;
}
int main()
{
cin >> s;
for (int i = 0; i <= 8; i++)
{
vis[0][i] = 1;
vis[8][i] = 1;
vis[i][0] = 1;
vis[i][8] = 1;
}
solve(1, 1, 0);
cout << ans << "\n";
}
Hope this helps!